堆排序怎么排

.example-btn{color:#fff;background-color:#5cb85c;border-color:#4cae4c}.example-btn:hover{color:#fff;background-color:#47a447;border-color:#398439}.example-btn:active{background-image:none}div.example{width:98%;color:#000;background-color:#f6f4f0;background-color:#d0e69c;background-color:#dcecb5;background-color:#e5eecc;margin:0 0 5px 0;padding:5px;border:1px solid #d4d4d4;background-image:-webkit-linear-gradient(#fff,#e5eecc 100px);background-image:linear-gradient(#fff,#e5eecc 100px)}div.example_code{line-height:1.4em;width:98%;background-color:#fff;padding:5px;border:1px solid #d4d4d4;font-size:110%;font-family:Menlo,Monaco,Consolas,"Andale Mono","lucida console","Courier New",monospace;word-break:break-all;word-wrap:break-word}div.example_result{background-color:#fff;padding:4px;border:1px solid #d4d4d4;width:98%}div.code{width:98%;border:1px solid #d4d4d4;background-color:#f6f4f0;color:#444;padding:5px;margin:0}div.code div{font-size:110%}div.code div,div.code p,div.example_code p{font-family:"courier new"}pre{margin:15px auto;font:12px/20px Menlo,Monaco,Consolas,"Andale Mono","lucida console","Courier New",monospace;white-space:pre-wrap;word-break:break-all;word-wrap:break-word;border:1px solid #ddd;border-left-width:4px;padding:10px 15px}

排序算法是《数据结构与算法》中最基本的算法之一。排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。以下是堆排序算法：

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

1. 算法步骤

创建一个堆 H[0……n-1]；

把堆首（最大值）和堆尾互换；

把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；

重复步骤 2，直到堆的尺寸为 1。

2. 动图演示

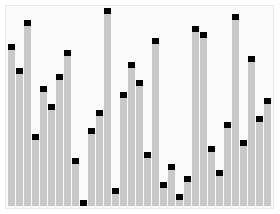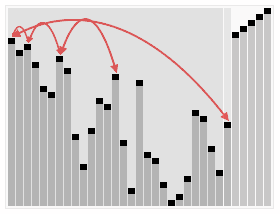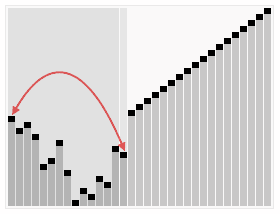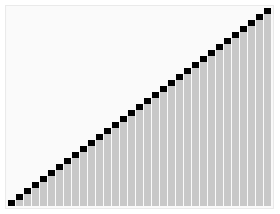
代码实现JavaScript 实例 var len;    // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量function buildMaxHeap(arr) {   // 建立大顶堆    len = arr.length;    for (var i = Math.floor(len/2); i >= 0; i--) {        heapify(arr, i);    }}function heapify(arr, i) {     // 堆调整    var left = 2 * i + 1,        right = 2 * i + 2,        largest = i;    if (left < len && arr[left] > arr[largest]) {        largest = left;    }    if (right < len && arr[right] > arr[largest]) {        largest = right;    }    if (largest != i) {        swap(arr, i, largest);        heapify(arr, largest);    }}function swap(arr, i, j) {    var temp = arr[i];    arr[i] = arr[j];    arr[j] = temp;}function heapSort(arr) {    buildMaxHeap(arr);    for (var i = arr.length-1; i > 0; i--) {        swap(arr, 0, i);        len--;        heapify(arr, 0);    }    return arr;}Python实例 def buildMaxHeap(arr):    import math    for i in range(math.floor(len(arr)/2),-1,-1):        heapify(arr,i)def heapify(arr, i):    left = 2*i+1    right = 2*i+2    largest = i    if left < arrLen and arr[left] > arr[largest]:        largest = left    if right < arrLen and arr[right] > arr[largest]:        largest = right    if largest != i:        swap(arr, i, largest)        heapify(arr, largest)def swap(arr, i, j):    arr[i], arr[j] = arr[j], arr[i]def heapSort(arr):    global arrLen    arrLen = len(arr)    buildMaxHeap(arr)    for i in range(len(arr)-1,0,-1):        swap(arr,0,i)        arrLen -=1        heapify(arr, 0)    return arrGo实例 func heapSort(arr []int) []int {        arrLen := len(arr)        buildMaxHeap(arr, arrLen)        for i := arrLen - 1; i >= 0; i-- {                swap(arr, 0, i)                arrLen -= 1                heapify(arr, 0, arrLen)        }        return arr}func buildMaxHeap(arr []int, arrLen int) {        for i := arrLen / 2; i >= 0; i-- {                heapify(arr, i, arrLen)        }}func heapify(arr []int, i, arrLen int) {        left := 2*i + 1        right := 2*i + 2        largest := i        if left < arrLen && arr[left] > arr[largest] {                largest = left        }        if right < arrLen && arr[right] > arr[largest] {                largest = right        }        if largest != i {                swap(arr, i, largest)                heapify(arr, largest, arrLen)        }}func swap(arr []int, i, j int) {        arr[i], arr[j] = arr[j], arr[i]}Java实例 public class HeapSort implements IArraySort {    @Override    public int[] sort(int[] sourceArray) throws Exception {        // 对 arr 进行拷贝，不改变参数内容        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);        int len = arr.length;        buildMaxHeap(arr, len);        for (int i = len - 1; i > 0; i--) {            swap(arr, 0, i);            len--;            heapify(arr, 0, len);        }        return arr;    }    private void buildMaxHeap(int[] arr, int len) {        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {            heapify(arr, i, len);        }    }    private void heapify(int[] arr, int i, int len) {        int left = 2 * i + 1;        int right = 2 * i + 2;        int largest = i;        if (left < len && arr[left] > arr[largest]) {            largest = left;        }        if (right < len && arr[right] > arr[largest]) {            largest = right;        }        if (largest != i) {            swap(arr, i, largest);            heapify(arr, largest, len);        }    }    private void swap(int[] arr, int i, int j) {        int temp = arr[i];        arr[i] = arr[j];        arr[j] = temp;    }}PHP 实例 function buildMaxHeap(&$arr){    global $len;    for ($i = floor($len/2); $i >= 0; $i--) {        heapify($arr, $i);    }}function heapify(&$arr, $i){    global $len;    $left = 2 * $i + 1;    $right = 2 * $i + 2;    $largest = $i;    if ($left < $len && $arr[$left] > $arr[$largest]) {        $largest = $left;    }    if ($right < $len && $arr[$right] > $arr[$largest]) {        $largest = $right;    }    if ($largest != $i) {        swap($arr, $i, $largest);        heapify($arr, $largest);    }}function swap(&$arr, $i, $j){    $temp = $arr[$i];    $arr[$i] = $arr[$j];    $arr[$j] = $temp;}function heapSort($arr) {    global $len;    $len = count($arr);    buildMaxHeap($arr);    for ($i = count($arr) - 1; $i > 0; $i--) {        swap($arr, 0, $i);        $len--;        heapify($arr, 0);    }    return $arr;}C实例 #include #include void swap(int *a, int *b) {    int temp = *b;    *b = *a;    *a = temp;}void max_heapify(int arr[], int start, int end) {    // 建立父節點指標和子節點指標    int dad = start;    int son = dad * 2 + 1;    while (son <= end) { // 若子節點指標在範圍內才做比較        if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的            son++;        if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數            return;        else { // 否則交換父子內容再繼續子節點和孫節點比較            swap(&arr[dad], &arr[son]);            dad = son;            son = dad * 2 + 1;        }    }}void heap_sort(int arr[], int len) {    int i;    // 初始化，i從最後一個父節點開始調整    for (i = len / 2 - 1; i >= 0; i--)        max_heapify(arr, i, len - 1);    // 先將第一個元素和已排好元素前一位做交換，再重新調整，直到排序完畢    for (i = len - 1; i > 0; i--) {        swap(&arr[0], &arr[i]);        max_heapify(arr, 0, i - 1);    }}int main() {    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };    int len = (int) sizeof(arr) / sizeof(*arr);    heap_sort(arr, len);    int i;    for (i = 0; i < len; i++)        printf("%d ", arr[i]);    printf(" ");    return 0;}C++实例 #include #include using namespace std;void max_heapify(int arr[], int start, int end) {    // 建立父節點指標和子節點指標    int dad = start;    int son = dad * 2 + 1;    while (son <= end) { // 若子節點指標在範圍內才做比較        if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的            son++;        if (arr[dad] > arr[son]) // 如果父節點大於子節點代表調整完畢，直接跳出函數            return;        else { // 否則交換父子內容再繼續子節點和孫節點比較            swap(arr[dad], arr[son]);            dad = son;            son = dad * 2 + 1;        }    }}void heap_sort(int arr[], int len) {    // 初始化，i從最後一個父節點開始調整    for (int i = len / 2 - 1; i >= 0; i--)        max_heapify(arr, i, len - 1);    // 先將第一個元素和已经排好的元素前一位做交換，再從新調整(刚调整的元素之前的元素)，直到排序完畢    for (int i = len - 1; i > 0; i--) {        swap(arr[0], arr[i]);        max_heapify(arr, 0, i - 1);    }}int main() {    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };    int len = (int) sizeof(arr) / sizeof(*arr);    heap_sort(arr, len);    for (int i = 0; i < len; i++)        cout << arr[i] << ' ';    cout << endl;    return 0;}

参考文章：

https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/7.heapSort.md

https://zh.wikipedia.org/wiki/%E5%A0%86%E6%8E%92%E5%BA%8F

以下是热心网友对堆排序算法的补充，仅供参考：

热心网友提供的补充1：

上方又没些 C# 的堆排序，艾孜尔江补充如下：

/// 

/// 堆排序
/// 
/// 待排序数组
static void HeapSort(int[] arr)
{
    int vCount = arr.Length;
    int[] tempKey = new int[vCount + 1];
    // 元素索引从1开始
    for (int i = 0; i < vCount; i++)
    {
        tempKey[i + 1] = arr[i];
    }
    // 初始数据建堆（从含最后一个结点的子树开始构建，依次向前，形成整个二叉堆）
    for (int i = vCount / 2; i >= 1; i--)
    {
        Restore(tempKey, i, vCount);
    }
    // 不断输出堆顶元素、重构堆，进行排序
    for (int i = vCount; i > 1; i--)
    {
        int temp = tempKey[i];
        tempKey[i] = tempKey[1];
        tempKey[1] = temp;
        Restore(tempKey, 1, i - 1);
    }
    //排序结果
    for (int i = 0; i < vCount; i++)
    {
        arr[i] = tempKey[i + 1];
    }
}
/// 

/// 二叉堆的重构（针对于已构建好的二叉堆首尾互换之后的重构）
/// 
/// 
/// 根结点j
/// 结点数
static void Restore(int[] arr, int rootNode, int nodeCount)
{
    while (rootNode <= nodeCount / 2) // 保证根结点有子树
    {
        //找出左右儿子的最大值
        int m = (2 * rootNode + 1 <= nodeCount && arr[2 * rootNode + 1] > arr[2 * rootNode]) ? 2 * rootNode + 1 : 2 * rootNode;
        if (arr[m] > arr[rootNode])
        {
            int temp = arr[m];
            arr[m] = arr[rootNode];
            arr[rootNode] = temp;
            rootNode = m;
        }
        else
        {
            break;
        }
    }
}

热心网友提供的补充2：

堆排序是不稳定的排序！

既然如此，每次构建大顶堆时，在 父节点、左子节点、右子节点取三者中最大者作为父节点就行。我们追寻的只是最终排序后的结果，所以可以简化其中的步骤。

我将个人写的 Java 代码核心放在下方，有兴趣的同学可以一起讨论下：

public int[] sort(int a[]) {
    int len = a.length - 1;    
    for (int i = len; i > 0; i--) {
        maxHeap(a, i);        
        //交换 跟节点root 与 最后一个子节点i 的位置        
        swap(a, 0, i);        
        //i--无序数组尺寸减少了 
    }  
    return a;
}

/**构建一个大顶堆（完全二叉树 ） 
* 从  最后一个非叶子节点  开始，若父节点小于子节点，则互换他们两的位置。然后依次从右至左，从下到上进行！ 
* 最后一个非叶子节点，它的叶子节点 必定包括了最后一个（叶子）节点，所以 最后一个非叶子节点是 a[（n+1）/2-1] 
 
* @param a 
* @param lastIndex 这个数组的最后一个元素 
*/
static void maxHeap(int a[], int lastIndex) {
    for (int i = (lastIndex + 1) / 2 - 1; i >= 0; i--) {
       //反正 堆排序不稳定，先比较父与左子，大则交换；与右子同理。（不care 左子与右子位置是否变了！） 
        if (i * 2 + 1 <= lastIndex && a[i] < a[i * 2 + 1]) {
            swap(a, i, i * 2 + 1);        
        }    
        if (i * 2 + 2 <= lastIndex && a[i] < a[i * 2 + 2]) {
            swap(a, i, i * 2 + 2);        
        }
    }
}

private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

以上为堆排序算法详细介绍，插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等排序算法各有优缺点，用一张图概括：

关于时间复杂度

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

n：数据规模

k："桶"的个数

In-place：占用常数内存，不占用额外内存

Out-place：占用额外内存

稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同